#
Линейная балансировка
#
Для чего нужен модуль?
Модуль линейной балансировки необходим для построения сбалансированных разрезов и восстановления структуры к исходному недеформированному состоянию. Эти подходы являются наиболее эффективными при доказательстве или опровержении структурно-геологической интерпретации разреза. Они позволяют уменьшить количество возможных интерпретаций и, тем самым, снизить риски при проведении буровых работ. Данный модуль используется при работе со складчато-надвиговыми структурами, где проявлены деформации межслоевого скольжения.
#
Теория
#
Сбалансированный разрез
Сбалансированный разрез представляет собой обоснованную интерпретацию геологической структуры, которую можно корректно восстановить до исходного недеформированного состояния, сохраняя длину и мощность слоев без пропусков и перекрытий горизонтов.
Идея проведения линейной балансировки разрезов возникла в 1960-х годах при изучении Канадских Скалистых гор (например, работы Bally et al., 1966; Dahlstrom, 1970; Price and Mountjoy, 1970). С тех пор сбалансированные разрезы получили широкое применение, так как они эффективно помогают проверить модели геологической интерпретации разрезов и корректно оценить структуры на глубине, что является необходимым требованием как в разведочных, так и в научных целях.
Клинт Дальстром (1969) сформулировал ключевые положения построения сбалансированных разрезов, где он наилучшим образом описал их полезность и ограничения. Он подчеркнул, что хотя эти разрезы не всегда гарантируют полностью верную структурную интерпретацию, несбалансированные разрезы определенно не способны ее гарантировать.
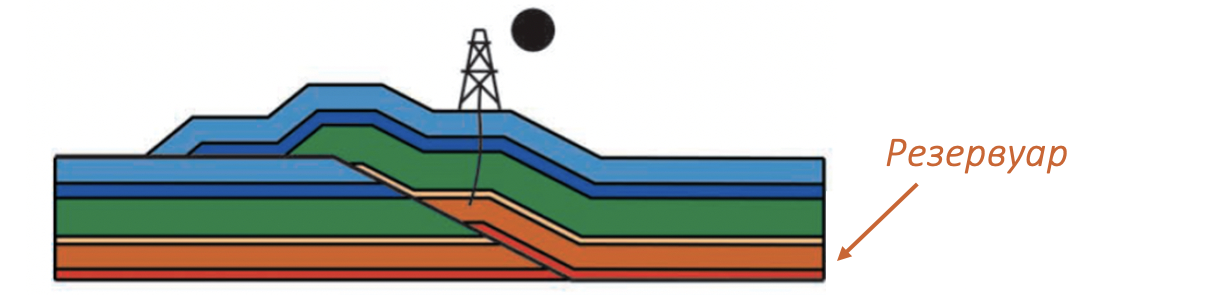
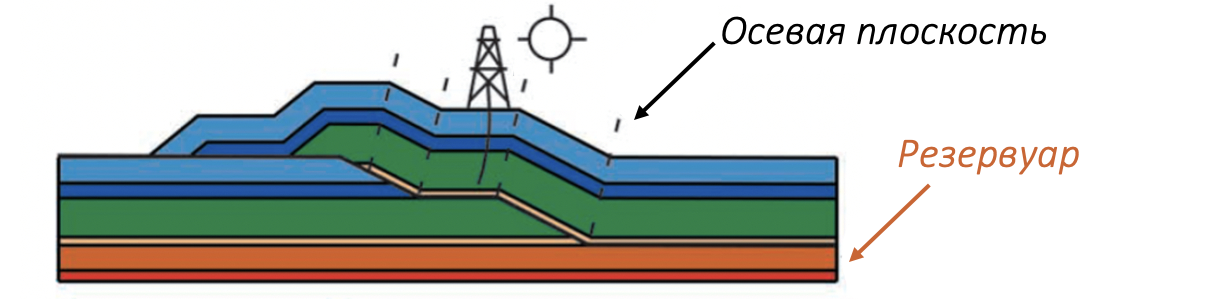
Эффективность применения сбалансированных разрезов наглядно демонстрируется в работе Скотта Вилкерсона и Кони Дикена, опубликованной в журнале AAPG Bulletin (2001). В их исследовании представлены типичные проблемы интерпретации складчато-надвиговых структур, требующие пересмотра и переинтерпретации. Один из таких примеров приведен в таблице ниже.
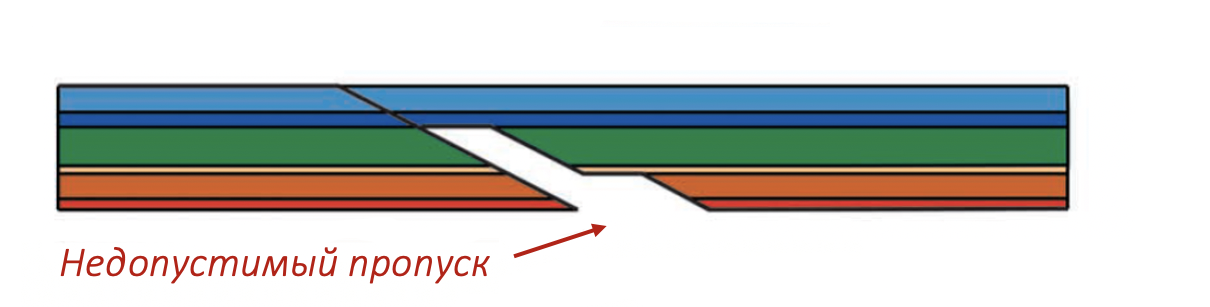
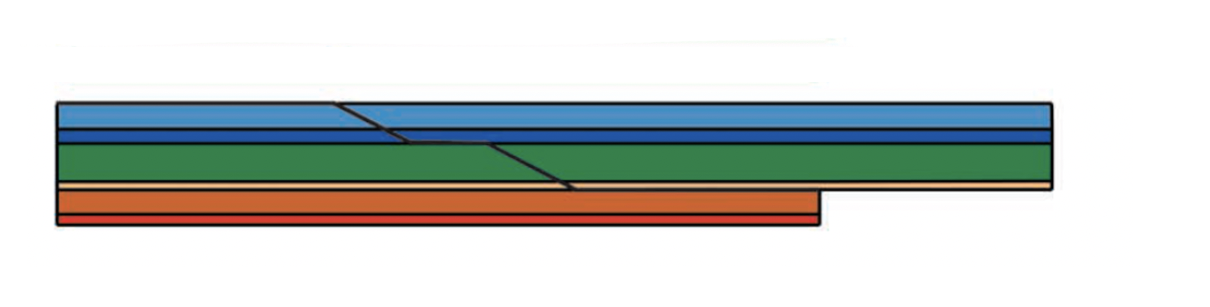
На исходной интерпретации видно, что число рамп висячего крыла разлома не соответствует числу рамп лежачего крыла. По этой причине, при восстановлении данной структуры присутсвует недопустимый пропуск, который делает исходную интерпретацию разреза некорректной, то есть несбалансированной. Для того чтобы разрез был сбалансирован необходимо скорректировать число рамп в лежачем крыле разлома таким образом, чтобы оно соответствовало числу рамп в висячем крыле. В этом примере перспективная скважина становится сухой, поскольку балансировка показывает, что резервуар (оранжевый слой) не вовлечен в складчатость.
Линейная балансировка является одним из наиболее популярных методов балансировки разрезов при решении практических задач. Тем не менее, важно учитывать следующие геологические ситуации (Allmendinger, 2019) в которых применение данного метода может быть ограничено или невозможно:
- Образование разломов синхронное осадконакоплению
- Уплотнение осадков в процессе деформации (особенно актуально в аккреционных призмах и толщах предгорных бассейнов)
- Растворение под давлением карбонатных или кремнистых пород
- Внедрение интрузивных комплексов
- Развитие рамп по латерали
- Региональная сдвиговая тектоника
Помимо линейной балансировки разрезов, существуют подходы к построению сбалансированных разрезов по площади, где предполагается, что площади литолого-стратиграфических подразделений не изменяются в процессе деформации. Эти подходы могут применяться для всех типов структур концентрической складчатости, включая параллельные и подобные складки. Однако, в отличие от линейной балансировки, площадная балансировка не выявляет конкретные проблемы внутри разреза, а предоставляет общую оценку структуры. По этой причине такие подходы больше применяются в академической сфере, чем в производственной.
Балансировка разрезов по площади имеет частный случай, применяемый на практике для определения глубины до поверхности субгоризонтального срыва (Epard and Groshong, 1993). Для его использования требуется линейная балансировка изучаемого разреза.
На примере выше приведены исходный и восстановленный разрезы, опубликованные в книге Джона Рамзи и Мартина Хуберта (1987). Исходный разрез выглядит вполне естественным для фронтальной части складчато-надвиговых покровов. Однако, зигзагообразная форма разлома слева на восстановленном разрезе делает надвиговые перемещения по нему кинематически маловероятными. Это объясняется тем, что общее направление надвигов в исходной интерпретации должно соответствовать общему направлению надвигов в недеформированном состоянии. Следовательно, исходный разрез является несбалансированным и требует дальнейшей корректировки интерпретации.
#
Деформация межслоевого скольжения
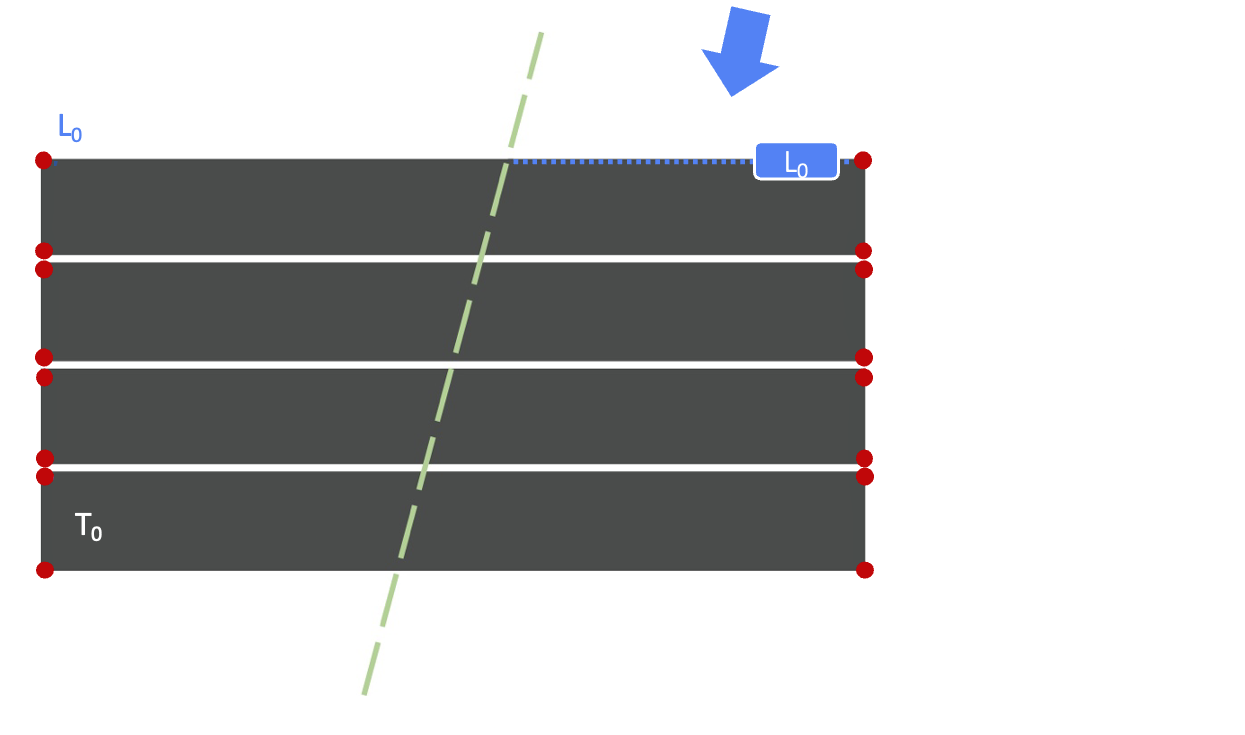
Линейная балансировка в основном применяется в складчато-надвиговых структурах, где проявлены деформации межслоевого скольжения (Woodward et al., 1989). Этот тип деформации характерен для концентрической складчатости, при которой образуются параллельные складки, сохраняющие длину и стратиграфическую мощность слоев в процессе их формирования (Ramsay and Huber, 1987).
При формировании параллельных складок длина и мощность недеформированного слоя (L0, T0) остаются равными длине и мощности деформированного слоя (L1, T1). Это происходит потому, что при деформации слои проскальзывают друг относительно друга, сохраняя при этом объем вещества. Расстояние между поверхностями скольжения может варьироваться от нескольких миллиметров до нескольких десятков метров (Shaw et al., 2005). Следовательно, в недеформированной части структуры отсутствует межслоевое скольжение, а его минимальное значение достигается в области перегиба складчатых структур (Groshong, 2006).
#
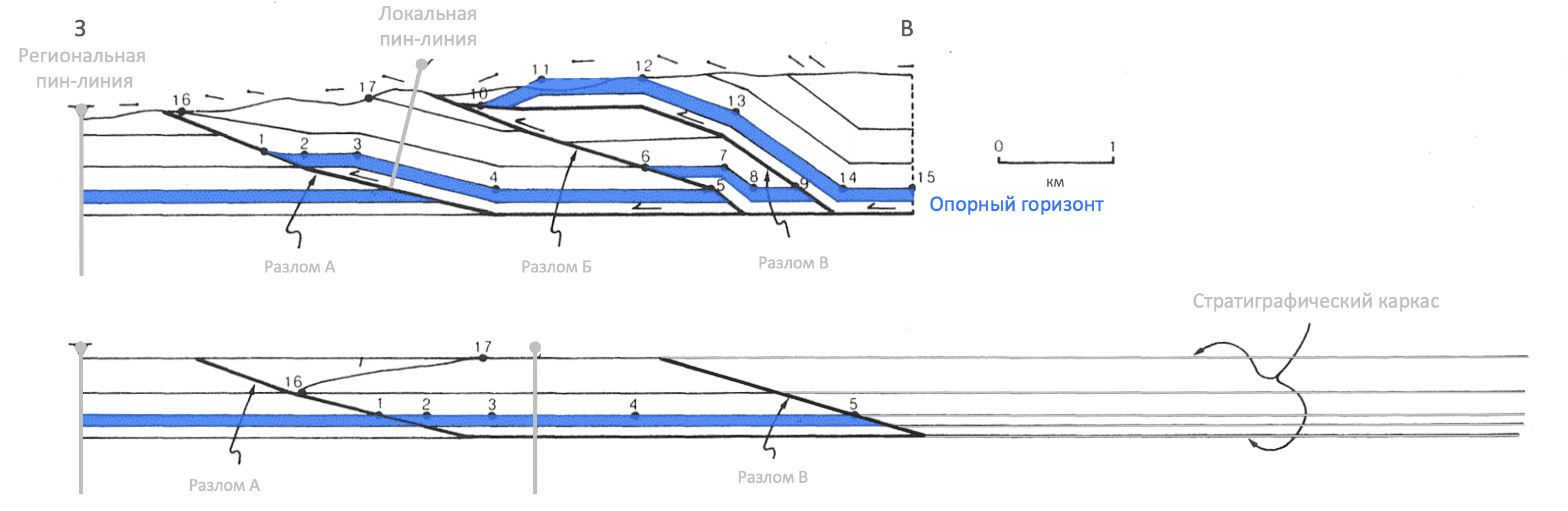
Пин-линия
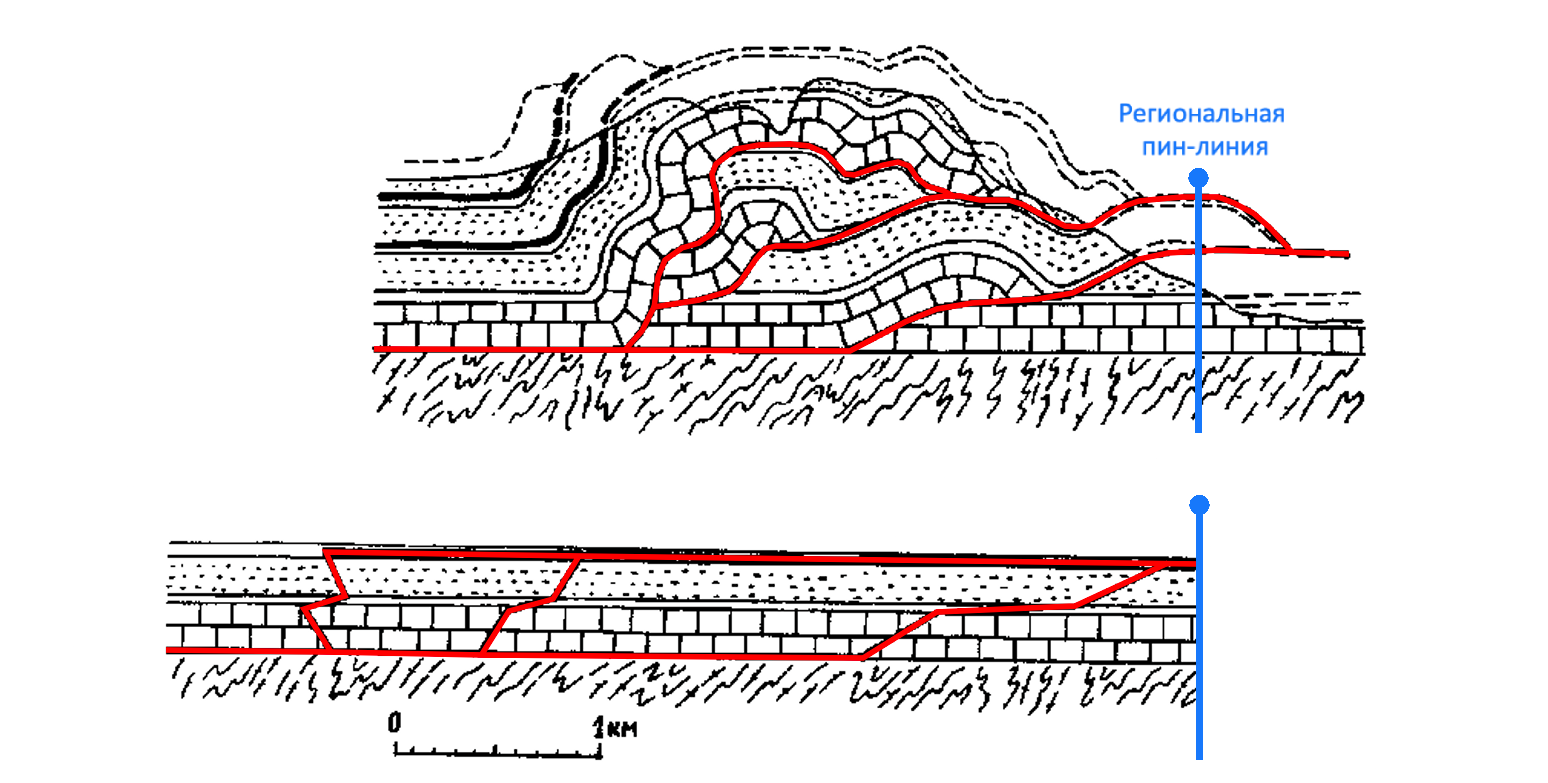
Пин-линия – это линия, относительно которой измеряется длина слоев и производится восстановление структуры (Dahlstrom, 1969).
В идельном случае используется Региональная пин-линия , которая устанавливается в недеформированной части краевого прогиба складчато-надвиговой системы. Это связано с тем, что в ней отсутствуют деформации межслоевого скольжения, а следовательно есть возможность зафиксировать положение слоев, которые не проскальзывали друг относительно друга.
Если исследуемый разрез не захватывает часть перед фронтом надвиговой системы, то следует использовать такой тип пин-линий, как Локальная пин-линия , которую желательно устанавливать на разрезе в области минимального межслоевого скольжения.
Классификация пин-линии как региональной или локальной определяется пользователем. В программе отсутствует специальное разделение на данные категории, и для создания пин-линии применяется инструмент Pin , который находится в панели инструментов.
В качестве примера ниже показана ориентировка пин-линий на исходном и частично восстановленном разрезах надвиговой структуры Пайн Маунтин в южных Аппалачах (Marshak and Mitra, 1988). Детальная балансировка этого разреза проводится в подразделе

Выбор ориентировки локальной пин-линии в плоскости разреза может быть затруднительным. На сегодня существуют следующие рекомендации (Dahlstrom, 1969; Woodward et al., 1989; Groshong, 2006; Allmendinger et al., 2012; Allmendinger, 2019), где локальная пин-линия может быть ориентирована:
- Вдоль осевой поверхности антиклинальных или синклинальных структур. Это подходит для складок с фиксированным шарниром, где значения межслоевого скольжения минимальны
- Перпендикулярно горизонтальному залеганию слоев, поскольку эти участки разреза могут оставаться недеформированными
- Вдоль линий разрывных нарушений или в их непосредственной близости
- С учетом углового сдвига деформации
На восстановленном разрезе пин-линии должны быть ориентированы перпендикулярно к слоистости, то есть вертикально.
Подробное описание данного вопроса приводится в учебнике Ричарда Альмендингера (Allmendinger, 2019). Здесь представлены основные вычисления и примеры из его работы.
Величина углового сдвига, \psi, зависит от угла падения слоистости, \delta, как для прямых складок перегиба, так и изогнутых.
Прямые складки перегиба (kink folds):
\displaystyle \psi=tan^{-1}\Bigg (2tan\bigg(\frac \delta 2\bigg)\Bigg)Изогнутые складки перегиба (curved hinges):
\displaystyle \psi=tan^{-1}(0.0175\delta)Графическое представление значения угла сдвига, \psi, в зависимости от угла падения слоистости, \delta, в диапазоне от 0 до 180 градусов (то есть от нормального до опрокинутого залегания) можно выразить следующим образом:
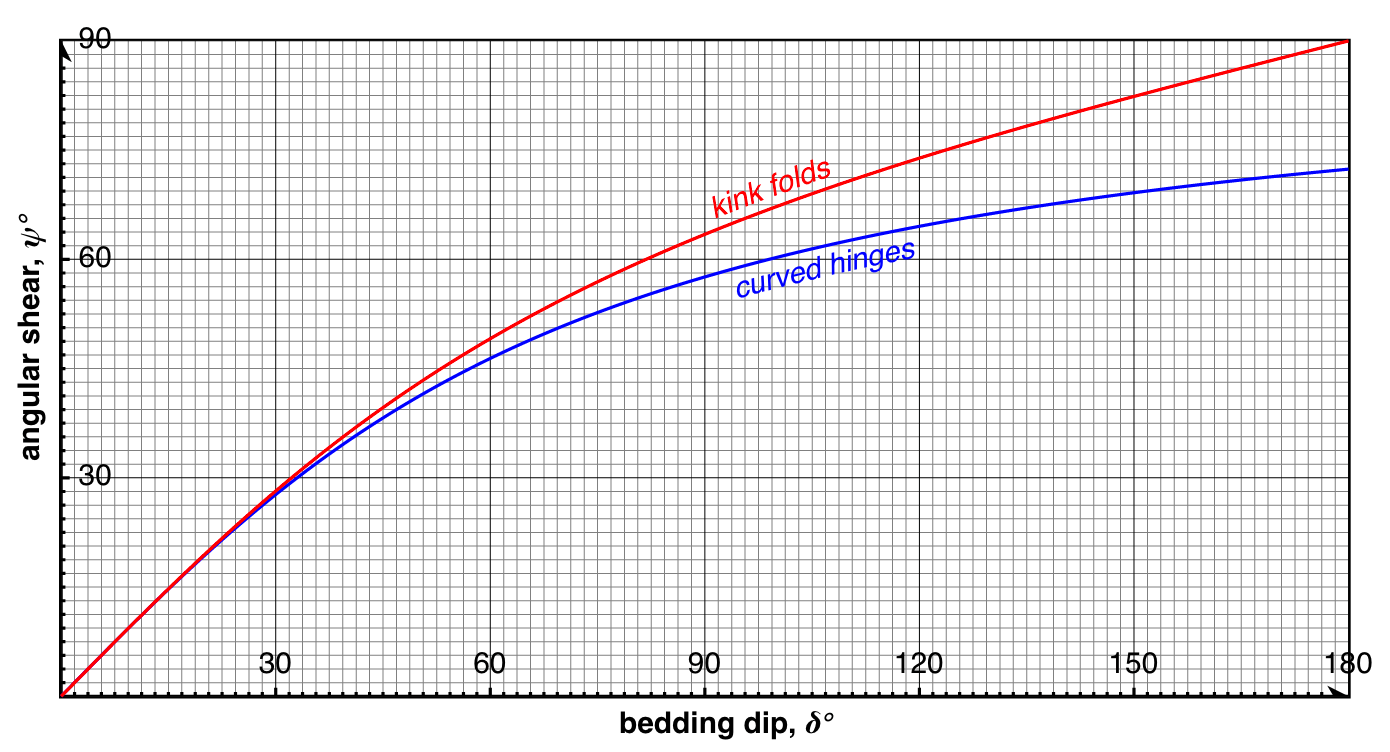
Величина углового сдвига, \psi, может быть использована для ориентировки локальной пин-линии при восстановлении надвиговых структур, например, с эродированными срезами висячих блоков.
Ниже представлена исходная модель, на которой отображено деформированное состояние разреза. Также показаны три возможных ориентировки локальных пин-линий – A, B и C для восстановления данной структуры. Угол \psi соответствует угловому сдвигу, рассчитанному для имеющегося падения слоистости, \delta, в неэродированной части висячего блока:
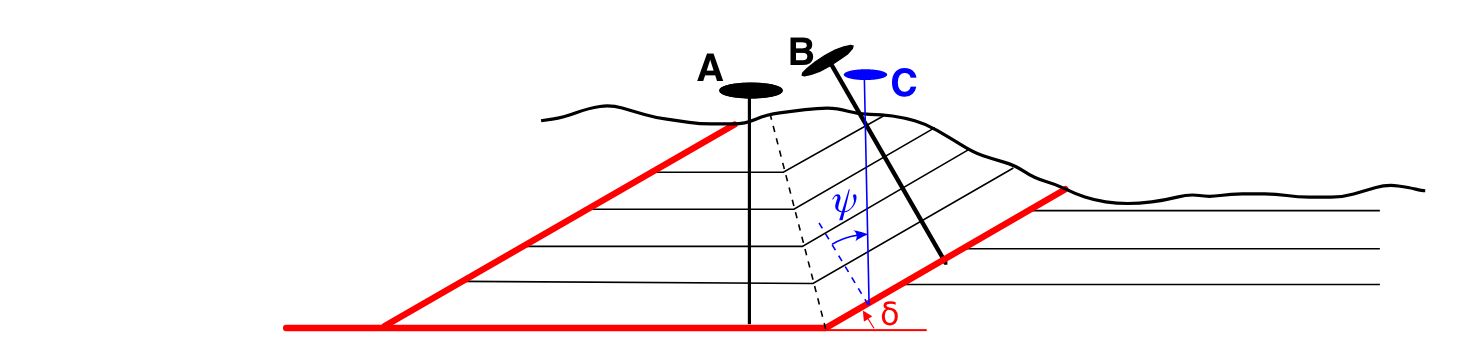
Восстановленный разрез по пин-линии А. Угол наклона рампа составляет 30° и соответствует исходной модели, поскольку пин-линия ориентирована перпендикулярно к слоистости в недеформированной части разреза, где отсутствует деформация межслоевого скольжения:
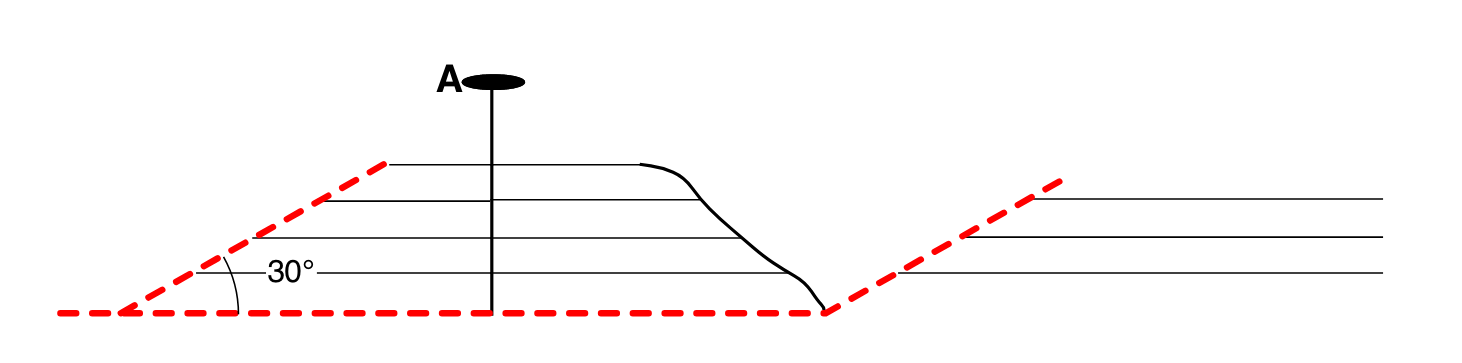
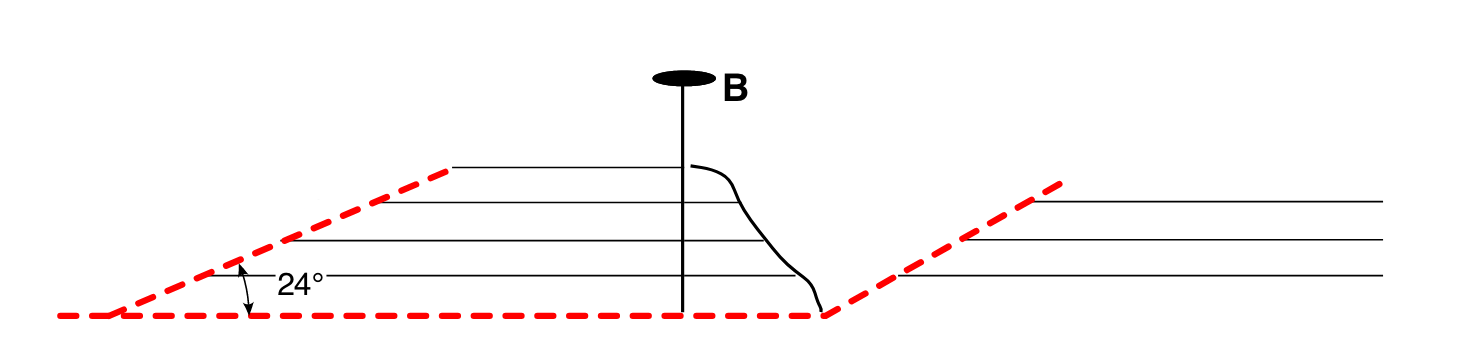
Восстановленный разрез по пин-линии B. Угол наклона рампа составляет 24°, так как пин-линия B предполагает отсутствие углового сдвига в наклоненном блоке и ориентирована перпендикулярно слоистости. Это некорректный выбор пин-линии, так как в этом блоке присутствует угловой сдвиг:
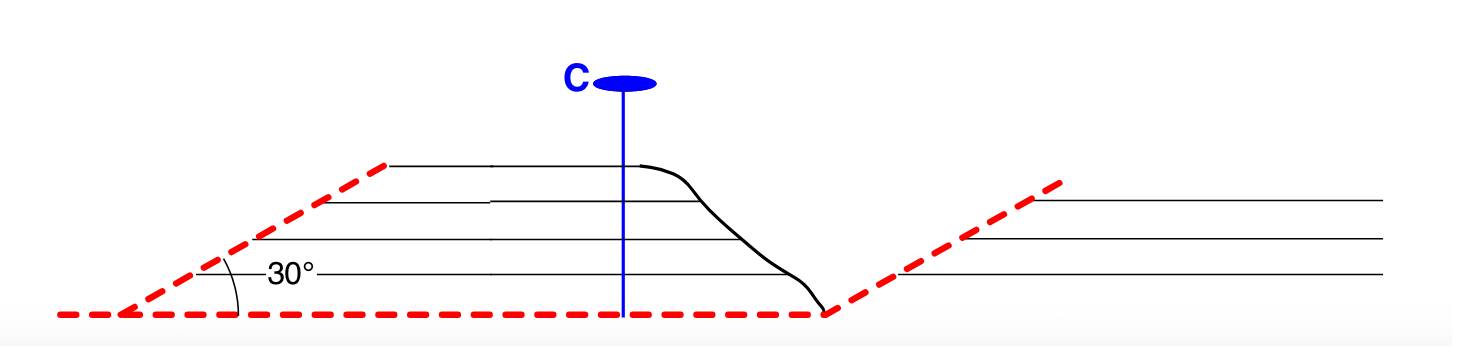
Восстановленный разрез по пин-линии С. Угол наклона рампа составляет 30° и отвечает исходной модели, так как пин-линия ориентирована с учетом углового сдвига, \psi, в наклоненном блоке. Это корректный выбор пин-линии, так как данная ориентировка отвечает минимальному межслоевому скольжению в крыле складки:
#
Опорный горизонт
Опорный горизонт – это горизонт, который ориентирован горизонтально и имеет бесшовное соединение на восстановленном разрезе. Он должен присутствовать в каждом разломном блоке, структуру которого требуется восстановить c использованием нескольких пин-линий (Groshong, 2006).
При выборе опорного горизонта рекомендуется (Woodward et al., 1989):
- Выбирать наиболее надежные горизонты, для которых имеются подтвержденные данные по скважинам и/или полевым наблюдениям
- Выбирать горизонты, соответствующие компетентным слоям, так как их прочностные свойства могут определять характер складчатых деформаций
- Не выбирать горизонты, большая часть которых на исследуемых разрезах эродирована
- Не выбирать горизонты, соответствующие слоям с высокой вязкостью и пластичностью, таким как глины, сланцы, аргиллиты и другие
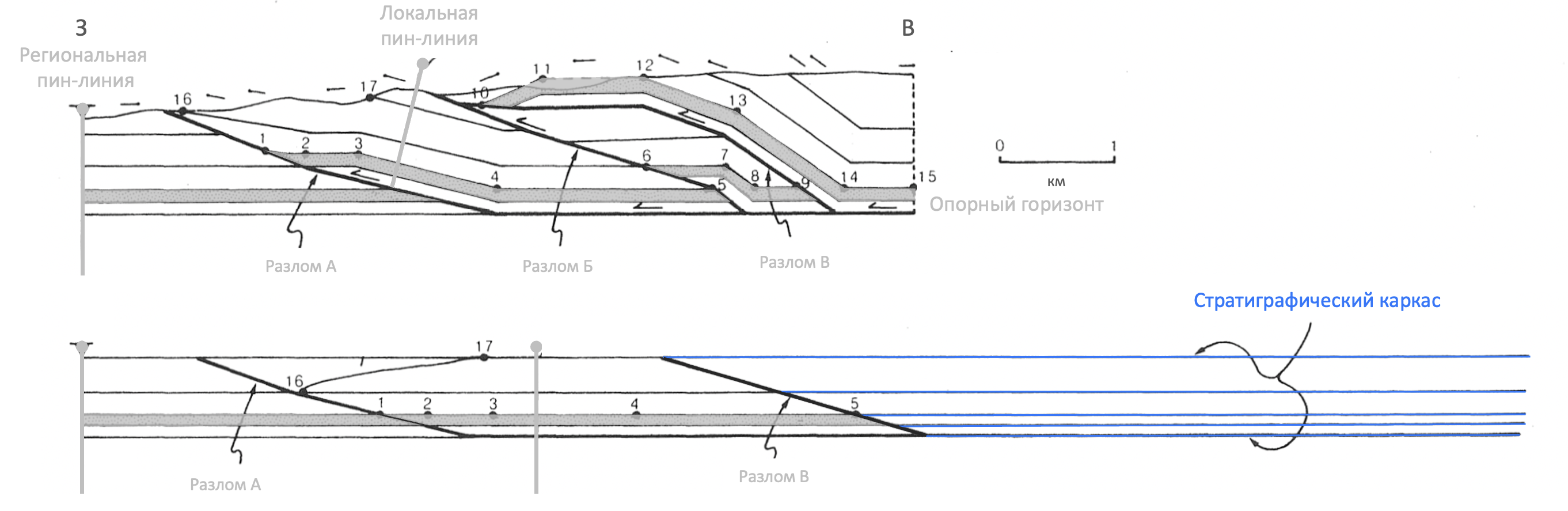
В качестве примера ниже показан выбор опорного горизонта на исходном и частично восстановленном разрезах надвиговой структуры Пайн Маунтин в южных Аппалачах (Marshak and Mitra, 1988). Детальная балансировка этого разреза проводится в подразделе
#
Стратиграфический каркас
Стратиграфический каркас – это недеформированная стратиграфическая последовательность, используемая для восстановления исследуемой структуры (Marshak and Mitra, 1988).
При балансировке разрезов стратиграфический каркас позволяет наглядно оценить исходную модель осадконакопления, которая может характеризоваться как постоянной мощностью, так и наличием
В качестве примера ниже показан стратиграфический каркас на частично восстановленном разрезе надвиговой структуры Пайн Маунтин в южных Аппалачах (Marshak and Mitra, 1988). Детальная балансировка этого разреза проводится в подразделе
#
Рабочий процесс
#
Компоненты модуля
Модуль линейной балансировки включает следющие компоненты:
#
Региональная пин-линия
Восстановление структуры с использованием только одной пин-линии осуществляется с помощью
В качестве примера работы с региональной пин-линией используется геологический разрез по центральным Аппалачам, опубликованный в исследовании Винтона Гвинна (Gwinn, 1964). В разрезе представлены региональные структуры антиклиналей Браун и Виллс, а также недеформированная часть складчато-надвигового комплекса.
Процесс работы сводится к выбору положения региональной пин-линии и последовательному восстановлению трех разломных блоков.
#
Определение пин-линии и восстановление первого разломного блока
Региональная пин-линия ориентирована перпендикулярно к слоистости в недеформированной части передового прогиба надвиговой структуры, так как в этой области отсутствуют деформации межслоевого скольжения.
Все стратифицированные объекты, которые пересекает пин-линия, автоматически добавляются в список объектов для восстановления.
Первый восстановленный разломный блок отображается на
При линейной балансировке разрезов стратиграфическая мощность не обязательно должна быть постоянной, она может изменяться в основании разреза. Примеры работы с такими структурами приведены в разделах
#
Восстановление остальных разломных блоков
В процессе балансировки второго разломного блока была ошибочно добавлена линия кровли Om. Чтобы исправить эту ошибку, можно удалить некорректно развернутый блок и восстановить структуру повторно без лишней линии. После этого можно восстановить недеформированную геометрию горизонтов третьего разломного блока и нарисовать положение восстановленных разломов.
Линии восстановленных разломов не создаются автоматически, так как этот процесс требует геологического понимания и интерпретации результатов.
При сохранении реконструкции создается пользовательская группа, где все новые созданные объекты имеют название исходных линий, дублируя их с префиксом Развернутая линия . Полученные объекты можно переместить внутри рабочего пространства или экспортировать в другую программу.
Основным условием линейной балансировки разрезов является равенство длин линий деформированных горизонтов длинам линий недеформированных, то есть развернутых горизонтов. Длину каждого линейного объекта можно посмотреть в их свойствах.
В данном примере видно, что исходная интерпретация требует небольшой корректировки, так как в правой части восстановленного разреза наблюдается неприемлемое зигзагообразное положение границ. При восстановлении сбалансированного разреза граница разломного блока справа должна быть ровной или наклоненной в одном направлении. Однако, Винтон Гвинн в любом случае опередил свое время, представив одну из первых структурных интерпретаций Центральных Аппалачей, которая до сих пор остается классическим примером при изучении этого региона.
Сохранить проектный файл разреза по Центральным Аппалачам можно в разделе
#
Локальная пин-линия
#
Восстановление разреза с постоянной истинной мощностью
В качестве примера используется упрощенный разрез надвиговой структуры Пайн Маунтин в Южных Аппалачах, который опубликован в учебнике Стивена Маршака и Гаутамы Митры (1988). В данном разрезе показаны четыре разломных блока и, соответственно, три надвига, которые соединяются с субгоризонтальным базальным срывом. На восстановленном разрезе заметны эродированные области, характеризующиеся большими промежутками между восстановленными в верхней части разреза горизонтами голубого и зеленого цвета.
При восстановлении структуры использовались
- Региональная пин-линия, установлена в первом недеформированном разломном блоке
- Локальная пин-линия, установлена во втором блоке и ориентирована перпендикулярно к слоистости в крыле взбросо-складки. При восстановлении этого блока используется пин-линия, так как верхняя часть разломного блока была эродирована и информация о геометрии голубого и зеленого горизонтов потеряна. Без использования пин-линии данный блок невозможно развернуть
- Восстановление дуплекса осуществляется без использования пин-линий
- Локальная пин-линия, используется в четвертом разломном блоке и ориентирована в шарнире взбросо-складки, где возможны минимальные значения межслоевого скольжения
Сохранить проектный файл разреза Южных Аппалачей можно в разделе
В текущей версии программы
Перед началом реконструкции для ручного выбора опорного горизонта необходимо восстановить временный разломный блок, в котором будет присутствовать только один горизонт. Именно этот горизонт будет использоваться в качестве опорного.
Ручной выбор опорного горизонта (голубой горизонт):
Выбор опорного горизонта по умолчанию (самый нижний горизонт):
#
Восстановление разреза с переменной истинной мощностью в основании разреза
В данном примере демонстрируется процесс восстановления части структуры Маунт Кранделл Дуплекс в Северных Кордильерах. Этот разрез впервые составил Роберт Джон Уилсон Дуглас (1952), а позднее восстановили Стивен Бойер и Дэвид Эллиотт (1982). Разрез характеризуется линейным увеличением истинной мощности с северо-востока на юго-запад в его основании, что указывает на наличие стратиграфического клина.
При восстановлении структуры использовались две локальные
В программе пин-линия всегда фиксирует стратиграфическую мощность и отображает ее на
К началу демонстрации все разломные блоки, кроме последнего на юго-западе, были восстановлены, а также отрисованы соответствующие им разломы. При добавлении последнего блока, между двумя пин-линиями в основании разреза происходит изменение истинной мощности и, как следствие, изменение стратиграфического каркаса. Отрисовка восстановленных разломов последнего блока указывает на возможность улучшения интерпретации исходного разреза. Например, можно добавить горизонт uA в дуплекс перед крайним слева разломным блоком и немного увеличить длину горизонта W, изменив геометрию самого крайнего слева надвига.
Сохранить проектный файл этого разреза можно в разделе
#
Стратиграфический клин
В этом разделе рассматривается процесс восстановления стратиграфического клина с помощью одной пин-линии. В качестве примера используется одна из моделей, представленных в работе Стивена Лингри и Оскара Видал-Ройо (2015), где наглядно проиллюстрирована разница в результатах восстановления одной и той же структуры при различном положении пин-линии.
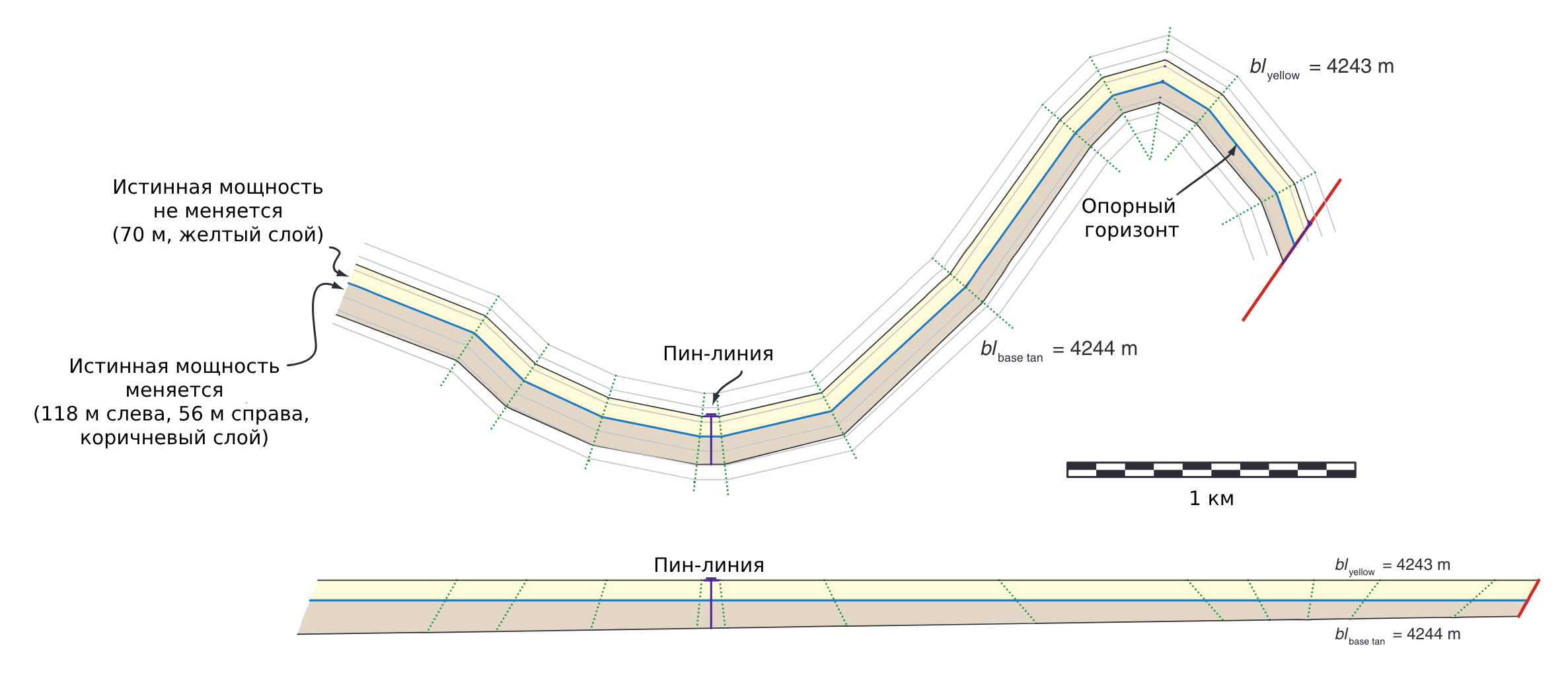
В данной модели имеется три горизонта в деформированном и восстановленном состояниях:
- Желтый горизонт соответствует кровле желтого слоя с постоянной истинной мощностью 70 метров. Длина горизонта составляет 4243 метра
- Синий горизонт является
опорным при восстановлении структуры - Коричневый горизонт соответствует подошве стратиграфического клина с переменной истинной мощностью от 118 метров на левом краю до 56 метров на правом краю. Длина горизонта составляет 4244 метра
#
Выбор опорного горизонта
В программе по умолчанию самый нижний горизонт на первом восстановленном блоке является опорным горизонтом. Подробнее об этом написано в разделе
После выбора
#
Восстановление структуры
После восстановления 5 блока с помощью пин-линии и определения стратиграфического каркаса, остальные 12 блоков восстанавливаются последовательно без использования пин-линий. Эти блоки соответствуют областям изгиба структуры.
Мощность
На восстановленном разрезе видно, что переменная истинная мощность стратиграфического клина не учтена. Это связано с тем, что восстановление структуры производилось только с одной пин-линией, которая установлена в 5 блоке.
#
Учет стратиграфического клина
Учет стратиграфического клина можно осуществить с помощью временных пин-линий и восстановленных блоков на краях структуры, где фиксируется корректная истинная мощность стратиграфического клина. На примере выше демонстрируется учет стратиграфического клина с переменной истинной мощностью от 118 метров на левом краю до 56 метров на правом краю:
- Для учета мощности стратиграфического клина на левом краю была установлена временная пин-линия в 1 блоке, где истинная мощность равняется 118 метрам
- На правом краю также можно было установить временную пин-линию и зафиксировать истинную мощность в 13 блоке, равную 56 метрам. Однако, не всегда есть возможность установить пин-линию для фиксации истинной мощности в деформированной структуре. Для таких случаев продемонстрирован процесс создания временного блока,где на правом краю установлена корректная истинная мощность каждого слоя, равная 70 и 56 метрам. Именно этот временный блок восстанавливается для учета стратиграфического клина
После восстановления структуры временные блоки следует удалить, так как они не отражают геологической интерпретации исходной модели и служат только для восстановления стратиграфического клина.
На восстановленном разрезе можно заметить, что большинство блоков, отвечающих областям изгиба структуры, соответствуют реконструкции в рассматриваемой модели. Однако, есть небольшие расхождения по коричневому горизонту с 9 по 13 блок, которые могут быть связаны с крупным масштабом изображения, где погрешность в несколько метров является допустимой.
Сохранить проектный файл этого разреза можно в разделе
Кроме того, в этом разделе можно сохранить проект, где представлен разрез структуры Маунт Кранделл Дуплекс в Северных Кордильерах (1982). В основании этого разреза наблюдается стратиграфический клин, который можно учесть также с помощью одной пин-линии при восстановлении структуры.
#
Примеры
#
Центральные Аппалачи
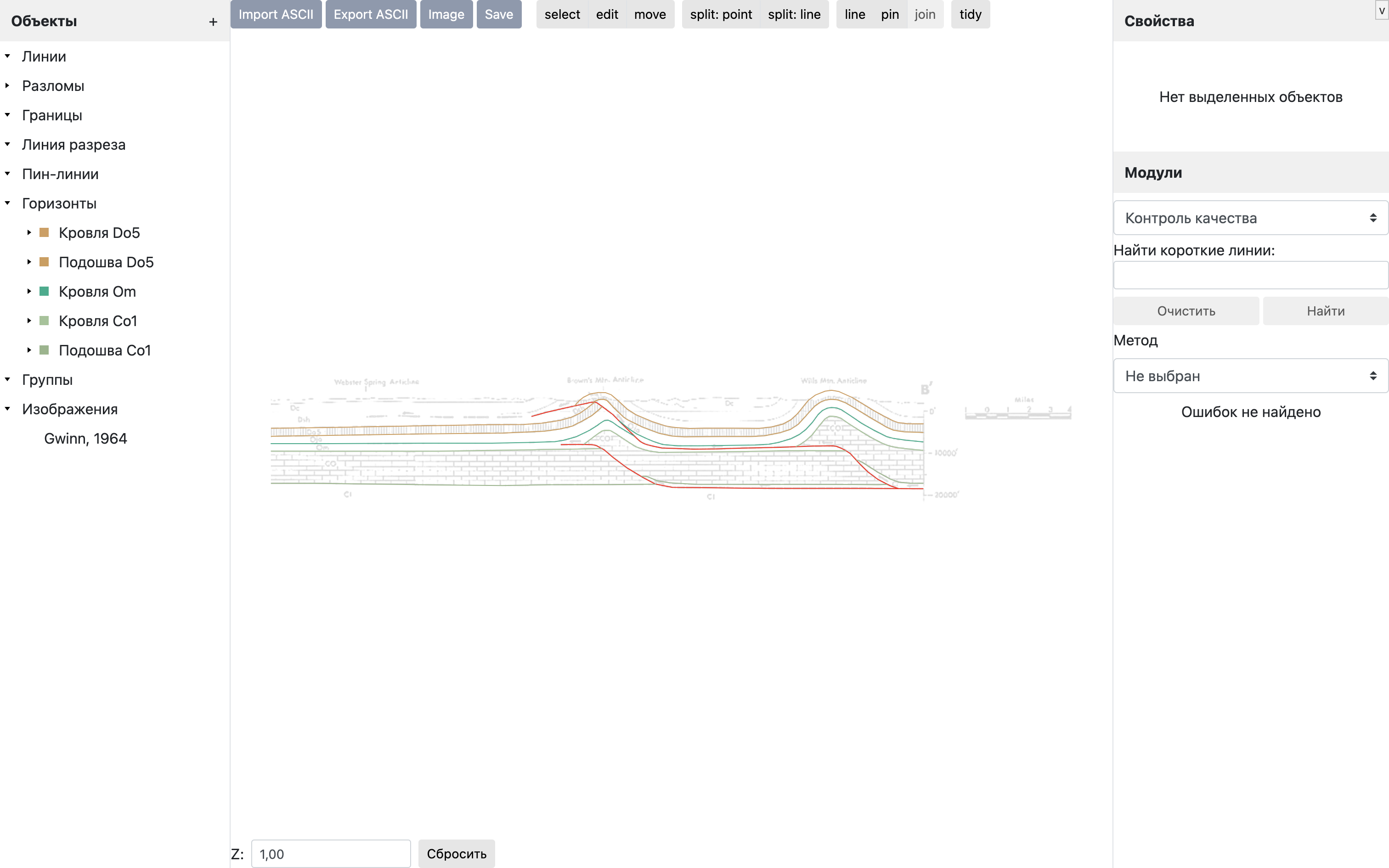
В проекте представлен разрез через Центральные Аппалачи, который был опубликован в работе Винтона Гвинна (Gwinn, 1964). В разрезе присутствуют региональные структуры антиклиналей Браун и Виллс, а также недеформированная часть складчато-надвигового комплекса.
Работа с разрезом приведена в разделе
#
Южные Аппалачи
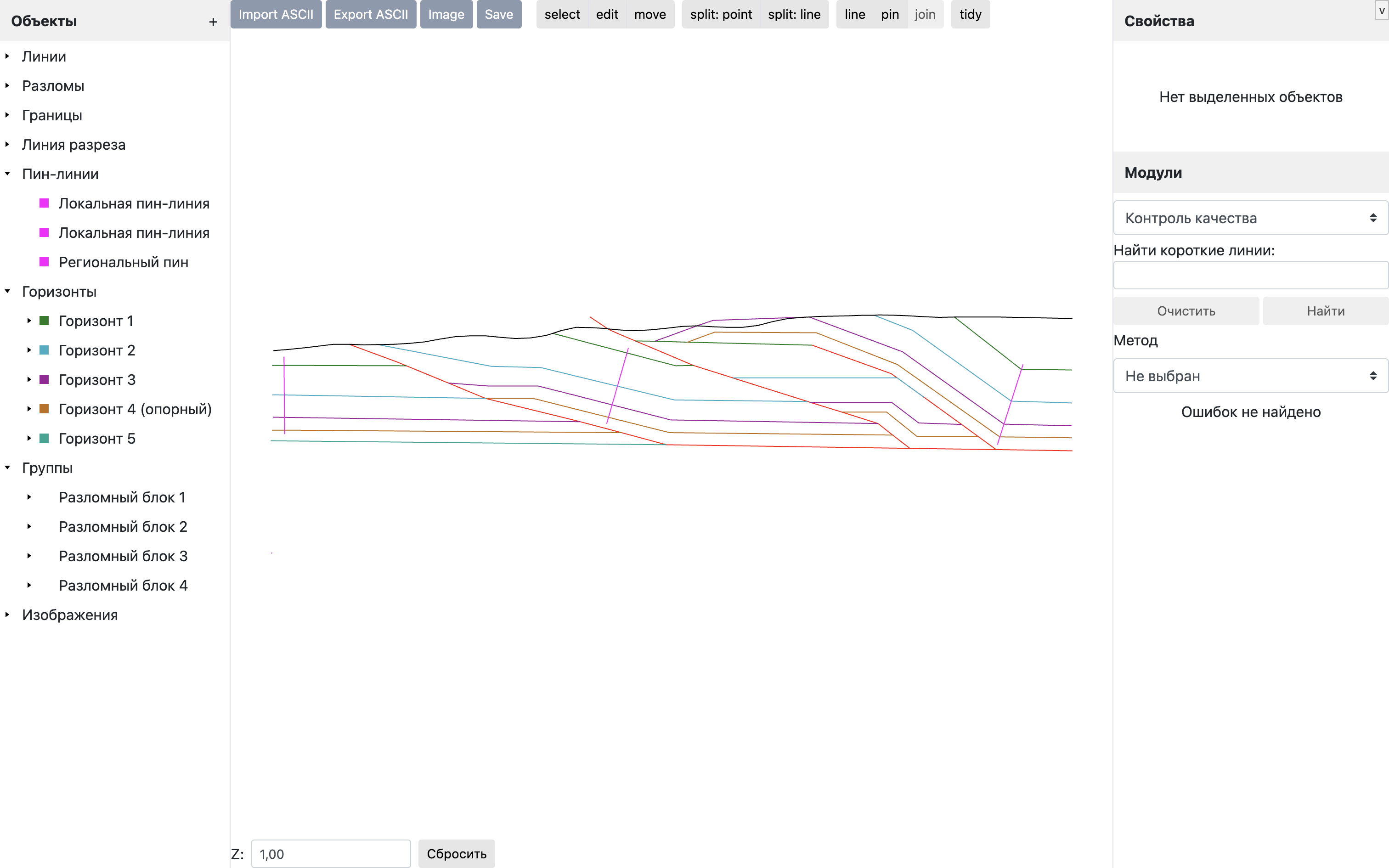
В проекте представлен упрощенный разрез надвиговой структуры Пайн Маунтин в Южных Аппалачах, который опубликован в учебнике Стивена Маршака и Гаутамы Митры (1988). В данном разрезе показаны четыре разломных блока и, соответственно, три надвига, которые соединяются с субгоризонтальным базальным срывом.
Работа с разрезом приведена в разделе
#
Северные Кордильеры
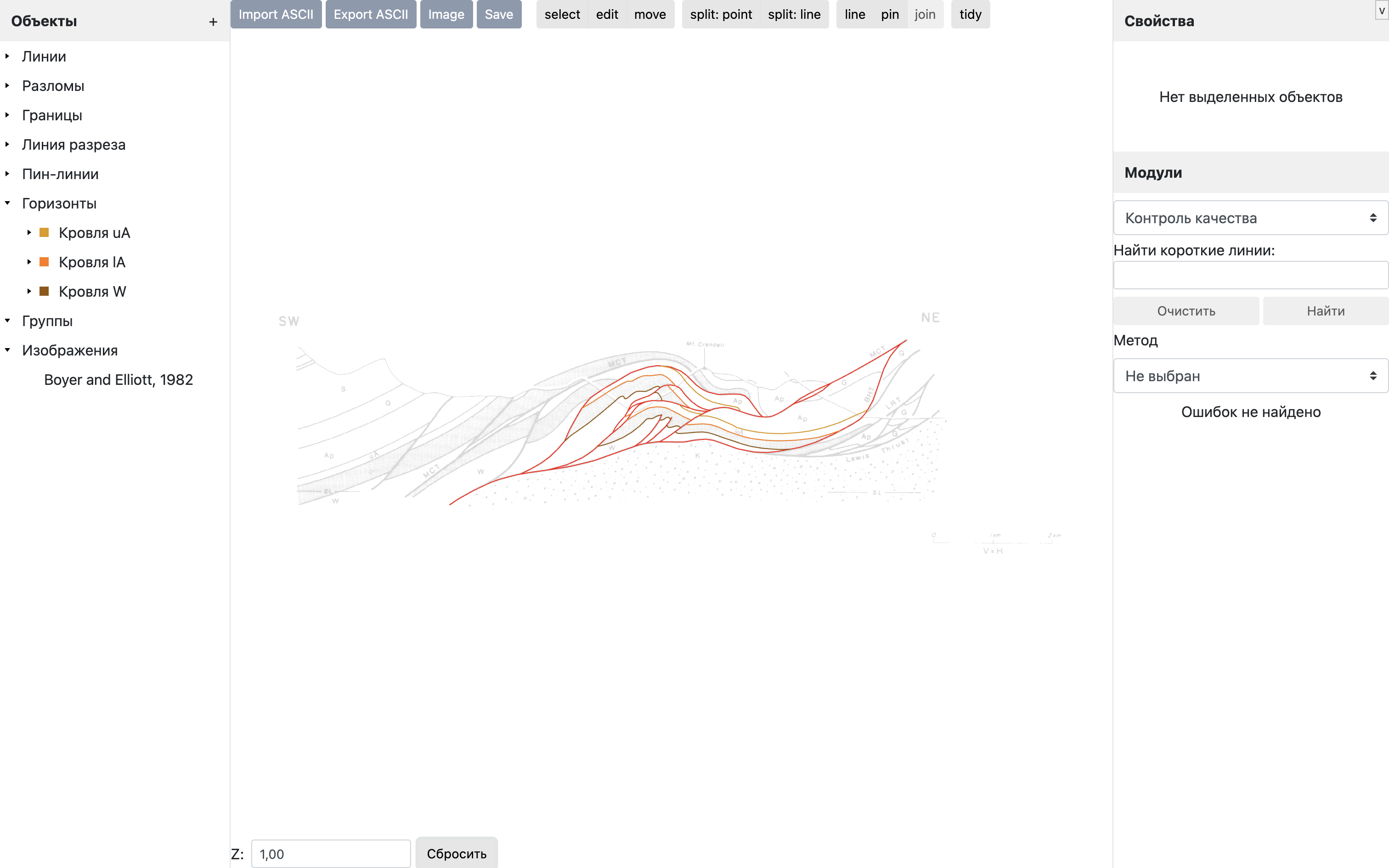
В проекте представлен разрез структуры Маунт Кранделл Дуплекс в Северных Кордильерах из работы Стивена Бойера и Дэвида Эллиотта (1982). Разрез характеризуется линейным увеличением истинной мощности с северо-востока на юго-запад в его основании, что указывает на наличие стратиграфического клина.
Работа с разрезом приведена в разделе
#
Стратиграфический клин
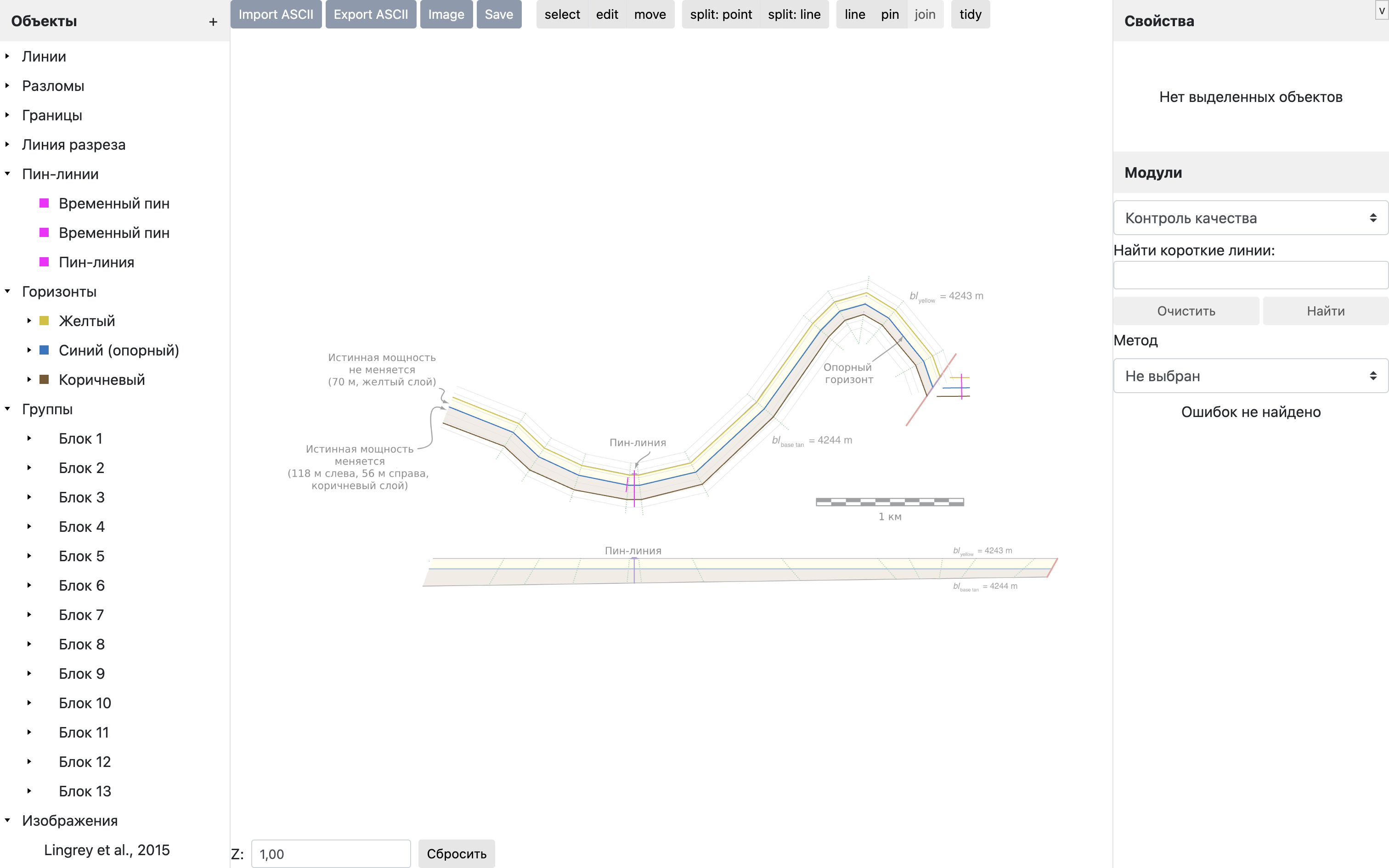
В проекте представлена теоретическая модель стратиграфического клина и одна из моделей его восстановления, опубликованная в работе Стивена Лингри и Оскара Видал-Ройо (2015).
Работа с разрезом приведена в разделе
#
Литература
- Allmendinger, R. W., Cardozo, N. C., and Fisher, D., 2012. Structural Geology Algorithms: Vectors & Tensors. Cambridge, England, Cambridge University Press, 289 pp.
- Allmendinger, R.W., 2019. Modern Structural Practice. A structural geology laboratory manual for the 21st Century. Online, 324 pp.
- Bally, A.W., Gordy, P.L., and Stewart, G.A., 1966. Structure, Seismic Data, and Orogenic Evolution of the Southern Canadian Rocky Mountains. Bulletin of Canadian Petroleum Geology 14, 337–381.
- Dahlstrom, C.D.A., 1969. Balanced cross sections. Canadian Journal of Earth Sciences 6, 743–757.
- Dahlstrom, C.D.A., 1970. Structural Geology on the Eastern Margin of the Canadian Rocky Mountains. Bulletin of Canadian Petroleum Geology 18, 332–406.
- Douglas, R.J.W., 1952. Preliminary Map, Waterton, Alberta. Geological Survey of Canada.
- Epard, J.L., Groshong, R.H., Jr., 1993. Excess Area and Depth to Detachment1. AAPG Bulletin 77, 1291–1302.
- Groshong, R.H., 2006. 3-D structural geology: A Practical Guide to Quantitative Surface and Subsurface Map Interpretation. Springer Berlin, Heidelberg, 400 pp.
- Gwinn, V.E., 1964. Thin-Skinned Tectonics in the Plateau and Northwestern Valley and Ridge Provinces of the Central Appalachians. Geological Society of America Bulletin 75, 863.
- Lingrey, S., Vidal-Royo, O., 2015. Evaluating the quality of bed length and area balance in 2D structural restorations. Interpretation 3, SAA133–SAA160.
- Marshak, S., Mitra, G., 1988. Basic methods of structural geology. Prentice Hall, Englewood Cliffs, 446 pp.
- Price, R. A., E. W. Mountjoy, 1970. Geologic structure of the Canadian Rocky Mountains between Bow and Athabasca rivers: A progress report. In J. O. Wheeler ed., Structure of the Southern Canadian Cordillera. Geological Association of Canada, 7–25.
- Ramsay, J.G., Huber, M.I., 1983. The Techniques of Modern Structural Geology Volume 2: Vol.2: Folds and Fractures. Academic Press, 700 pp.
- Shaw, J.H., Connors, C., Suppe, J., 2005. Seismic Interpretation of Contractional Fault-Related Folds. American Association of Petroleum Geologists (53), 58 pp.
- Steven E. Boyer, Elliott, D., 1982. Thrust Systems. AAPG Bulletin 66 (9), 1196–1230.
- Woodward, N.B., Boyer, S.E., Suppe, J., 1989. Balanced Geological Cross-Sections: An Essential Technique in Geological Research and Exploration. American Geophysical Union, Washington, D.C.
- Wilkerson, S., Connie, L., 2001. Quick-look techniques for evaluating two-dimensional cross sections in detached contractional settings. AAPG Bulletin 85 (10), 1759–1770.